
小学校6年生レベルの算数です。

さいころは、向かい合った(反対側)面の目の数の和が7になるようになっており、目の並び方は上の図のようになっています。
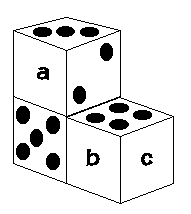
おなじさいころ3つを、上の図のように重ねました。
重ねあった(となりどうしの)さいころの合わさっている2つの面の目の数の和も、7になるようにしてあります。
この場合、(a)(b)(c)それぞれの目の数はいくつでしょうか。
解答はこの下 最後 ↓
◆作者のサイトです ちょっと一息 癒しのページ◆
65歳以上のパソコン愛好家の皆さんへ
いまさら人に聞くのも抵抗あり、よくあるパソコンセミナーに通う勇気もなく、なんとなくくずぶっている皆さん 皆さんにピッタリのWebサイトがありますよ!
『ゆったりパソコン』 ワード・エクセル・スマホの話題が続々アップされてます!
『ちかごろ考えること』 ゆっくりお茶を飲みながら覗いてみてください
時間のある時、一度訪問してみてください!

https://yyoweb.com/ ←こちらをクリック!
我が故郷 あさひ
朝日みどりの里(道の駅 朝日)
温泉もありますよ。ドライブの途中でちょっとひと風呂!!いいですよ (^^♪

<大前提>
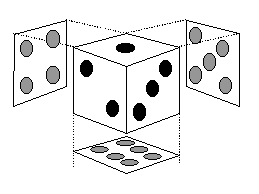
隠れている面の目の数は下のようになります。
それぞれ反対側の目の数と足すと7になるわけですね。
最初に(a)の目
右上のさいころの向きをかえて考えると 1である
次は(c)の目を
上段さいころの下面は4(3の反対側)ですから、それと合わさっている下段左さいころの上面は3
下段左さいころの5の面と3の面をヒントにして、(c)の反対側と合わさっている面は 1
ということは、(c)の反対側の面は 6
したがって(c)は 1
最後は(b)の目
4の面と(c)の1の面をヒントに向きを合わせると(b)は 2
<解答> (a)=1 (b)=2 (c)=1



